Phase unwrapping on reconfigurable hardware

Introduction

Over the past several years, the development of coherent imaging techniques has increased dramatically and now applications such as Magnetic Resonance Imaging (MRI) and Synthetic Aperture Radar are commonplace. At Northeastern University, a coherent imaging process known as Optical Quadrature Microscopy (OQM) has been developed for the purpose of non-invasively capturing the amplitude and phase data of an optically transparent sample. OQM is one of the modalities of the Keck 3D Fusion Microscope at Northeastern. With OQM, the phase is a property of a real signal related to the temporal and/or spatial wavelength and influences the signal only in range of the principal values, i.e. those lying in the range of (-p,p].

Sensors and basic signal processing produce a wrapped phase. This wrapping is a nonlinear process producing an output lying in the principal range of (-p,p]. To be able to generate an image, this wrapped output phase needs to be unwrapped. In the absence of noise, this unwrapping can be performed optimally by summing the wrapped phase differences (for the one dimensional case). This can be extended to the two-dimensional case by using a raster-scan approach. However, in the presence of noise, this method of unwrapping can fail catastrophically. More robust techniques have been proposed that unwrap around noisy sections thus preserving as much data as possible. Other methods that minimize noise through curve fitting and quality maps are also commonly utilized. The most significant drawback of using these advanced methods is that there is a high latency involved with processing the VGA quality (640x480) images produced by the CCD cameras. Thus some form of acceleration is necessary in order to get reasonable performance. Thus an implementation in hardware is being considered with the goal of eventually producing rapid, high quality phase-unwraps.

People

The following people have been involved in this project:

Professor Miriam Leeser

Professor Charles DiMarzio

Sherman Braganza

William Warger

Documents

1) Poster at CENSSIS site visit 2006

Phase 1: Analysis

Before the actual implementation is it necessary to determine which unwrapping algorithm produces the best results. A discussion of the quality of the images produced by the unwrap is here.

It is also necessary to determine the minimum bitwidth necessary to produce accurate results. This analysis is currently underway.

Phase 2: Initial Implementation

The core of the minimum L^P Norm algorithm is a 2D DCT. This transform consumes the largest part of the processing time and is thus a prime candidate for speedup. It will be the first segment implemented in hardware with support for full forward and reverse transforms.

One of the fastest ways to perform a 1-D DCT transform is to use Makhouls method. This involves using an FFT of the same size as the DCT, plus O(n) post-processing steps. The 1-D transform can easily be extended to two dimensions by performing the 1-D transform on the columns and then on the rows. An implementation of this algorithm is being worked on, and will be finalized once suitable bitwidths have been selected.

The hardware targeted for the implementation is the Annapolis Wildstar II Pro. An architectural diagram is given below:

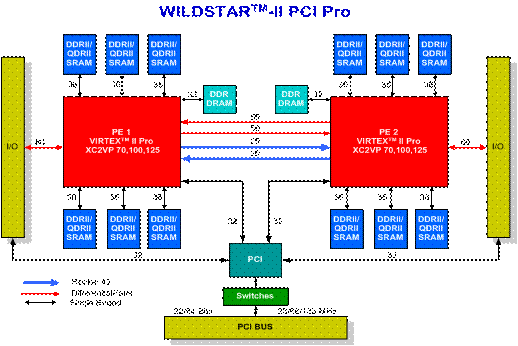
A short summary of the features that make this board suitable are given below:

• Uses two Xilinx® Virtex-II Pro™ FPGAs XC2V70 (33088 slices and 5904Kb BlockRAM)

• 12 ports of DDR II SRAM totally 48MBytes, 2 ports of DDR SDRAM totally 256 MBytes

• 11 GBytes/sec memory bandwidth