Analysis of Phase-Unwrap Quality of OQM Images

Over the past several years, the development of coherent imaging techniques has increased dramatically and now applications such as Magnetic Resonance Imaging (MRI) and Synthetic Aperture Radar are commonplace. At Northeastern University, a coherent imaging process known as Optical Quadrature Microscopy (OQM) has been developed for the purpose of non-invasively capturing the amplitude and phase data of an optically transparent sample [1]. The phase is a property of a real signal related to the temporal and/or spatial wavelength and influences the signal only in range of the principal values, i.e. those lying in the range of (-p,p].

Sensors and basic signal processing produce a wrapped phase. This wrapping is a nonlinear process producing an output lying in the principal range of (-p,p]. To be able to generate an image, this wrapped output phase needs to be unwrapped. In the absence of noise, this unwrapping can be performed optimally by summing the wrapped phase differences (for the one dimensional case). This can be extended to the two-dimensional case by using a raster-scan approach. However, in the presence of noise, this method of unwrapping can fail catastrophically. More robust techniques have been proposed that unwrap around noisy sections thus preserving as much data as possible. Other methods that minimize noise through curve fitting and quality maps are also commonly utilized. The most significant drawback of using these advanced methods is that there is a high latency involved with processing the VGA quality (640x480) images produced by the CCD cameras. Thus some form of acceleration is necessary in order to get reasonable performance.

As a preliminary step to the implementation of a phase-unwrapping algorithm on hardware (in this case a Field Programmable Gate Array or FPGA), it is necessary to verify the current choice of phase unwrapping algorithm used. This paper focuses on analyzing the tradeoffs between the different algorithms in Ghiglia and Pritt [2].

2.0 Methods used

The idea behind most phase-unwrapping algorithms is that the correct unwrapped phase varies slowly such that the gradient between pixels is less than a half-cycle, or p radians. If this assumption holds true, a wrapped signal may be unwrapped by simply summing until a gradient of |p| is reached at which point the phase is added to an integer multiple of p (2kp) and the summation continues. However, the problem is that if the data is noisy enough, phase gradients greater than p can lead to image corruption over large segments of the data. An example with an embryo and the Matlab ‘unwrap’ routine is shown below:

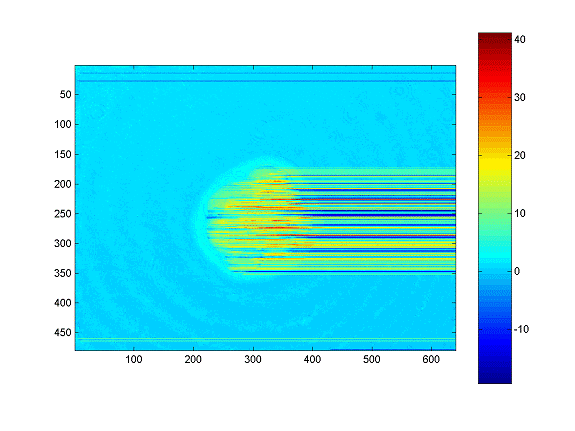
Figure 1: Raster unwrap using Matlab 'unwrap' routine

Given the failure of a straightforward integration when applied to noisy data, other methods utilizing residue detection/branch cuts, quality maps and error minimization are commonly used.

2.1 Path following

Path following algorithms solve the noisy data problem by selecting the path over which to integrate. Goldstein’s algorithm, one of the most common path-following algorithms, operates by identifying residues (points where the integral over a closed four pixel loop is non-zero) and connecting them via branch cuts or paths along which the integration path may not intersect.

One problem with Goldstein’s algorithm is that it does not utilize all the data available to guide the generation of branch cuts. By generating a map indicating the quality of the data over the image, it is possible to unwrap instances that cannot be done using Goldstein’s. These quality maps may be user-supplied or automatically generated using the pseudo-correlation, the variance of phase derivates or the maximum phase gradient.

Quality maps may be combined with branch cuts as in Goldstein’s algorithm to form a hybrid mask-cut method. The quality map is used to guide the placement of branch-cuts. Another approach was proposed by Flynn that detects discontinuities, joins them into loops and adds the correct multiple of 2p to it if the action removes more discontinuities than it adds. Flynn’s minimum discontinuity solution can also be used with a quality map to generate higher quality solutions.

2.2 Minimum-norm

This method of phase-unwrapping seeks to generate an unwrapped phase whose local phase derivatives match the measured derivates as closely as possible. This comparison can be defined as the difference between the two, raised to some power p.

The simplest method is the unweighted least squares algorithm. This family of methods uses Fourier or DCT techniques to solve the least squares problem but are vulnerable to noise. The pre-conditioned conjugate gradient (PCG) technique overcomes this problem by using quality maps to zero-weight noisy regions so that the unwrapped solution is not corrupted. There also exists a weighted multi-grid algorithm that uses a combination of fine and coarse grids to converge on a solution. Finally, the minimum L^P Norm algorithm solves the phase unwrapping problem for variable p. When p=2 it is the equivalent of a least squares unwrapping. When p=0 the algorithm minimizes the number of discontinuities in the unwrapped solution without concern for the magnitude of these discontinuities. This value of p generally produces the best solution. This algorithm can be used with or without user-supplied weights and for p<2, it also generates its own data-dependent weights. It iterates the PCG algorithm, which in turn iterates the DCT algorithm. This results in L^P Norm having among the highest costs of all the algorithms in terms of runtime and memory.

3.0 Results

The images in this report were generated at a resolution of 640x480 and were taken from the Keck microscope and from the OQM microscope set up by Bill Warger. They are all of Mouse 1 Embryo 11 and were taken in August ’04. All algorithms using a quality map were set-up to use the maximum phase gradient map [2] since it generally produces the best results [3]. The algorithms are presented below along with some characteristics:

Algorithm	Residue detection	Quality Map
Goldstein	Yes	No
Quality	No	Yes
Mask Cut	Yes	Yes
Flynn	No	Yes/ No
PCG	No	Yes
Multi-grid	No	Yes
L^pNorm	Yes	Yes/ No

3.1 Wrapped Phase

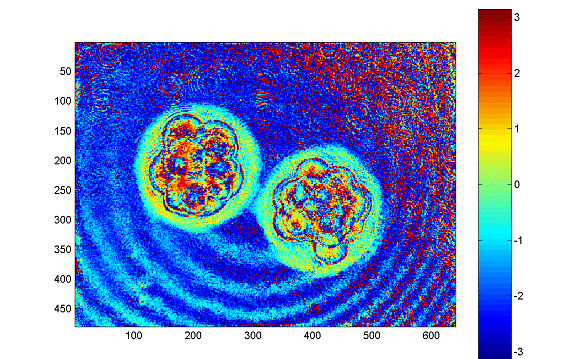
Figure 2: Embryo 11 wrapped

The wrapped data clearly demonstrates the problem. The phase can be observed to between -p and p and although the embryos are visible, the magnitude of the phase difference cannot be measured without an unwrapping.

3.2 Goldstein’s Algorithms

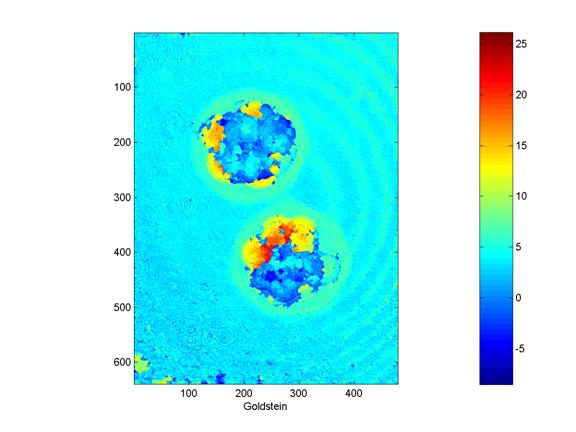
Figure 3: Goldstein’s Algorithm

In datasets with a large number of residues, Goldstein’s algorithm can place branch-cuts in such a way that they isolate portions of the image and thereby prevent the phase from being unwrapped over those segments. This is visible in the image above. However, Goldstein’s algorithm takes just a few seconds to execute thus making it among the fastest algorithms in this survey.

3.3 Full Multi-Grid (FMG)

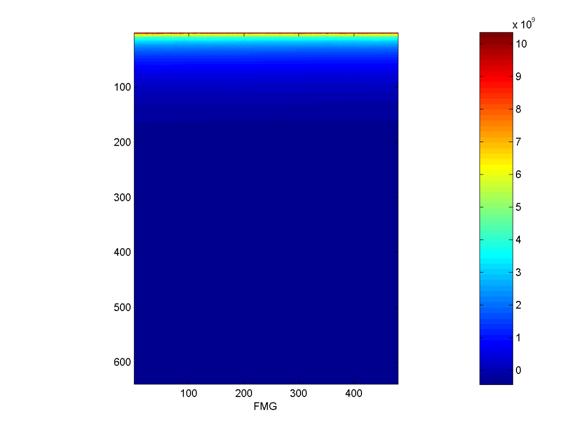
Figure 4: Full multi-grid (FMG) algorithm

The FMG algorithm consistently produces a banded solution as in Figure 4, with the correct phase range, but an incorrect distribution. This is true even of previous studies [3]. It is possible that this algorithm was incorrectly implemented. It will not be considered in further analyses.

3.4 Mask Cut Algorithm

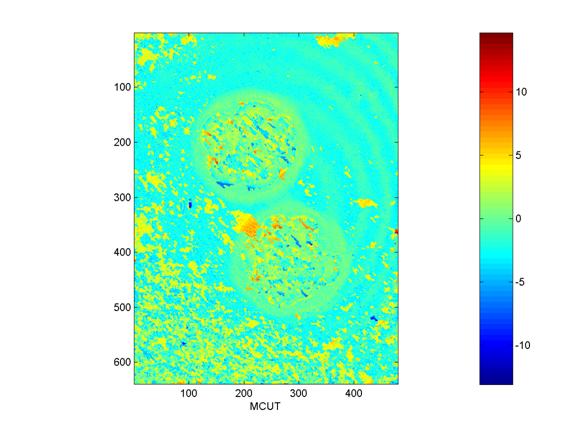
Figure 5: Mask Cut Algorithm

The mask cut algorithm produces diagonal flecking that is very noticeable across all unwraps. These flecks are created by the incorrect placement of branch cuts. Although it may seem that alternative quality mapping techniques would serve to eliminate image corruption that was not observed in my experiments and others [3]. The mask cut algorithm is the slowest algorithm among all the ones experimented with. Execution time on noisy data can take half an hour.

3.5 Preconditioned Conjugate Gradient (PCG)

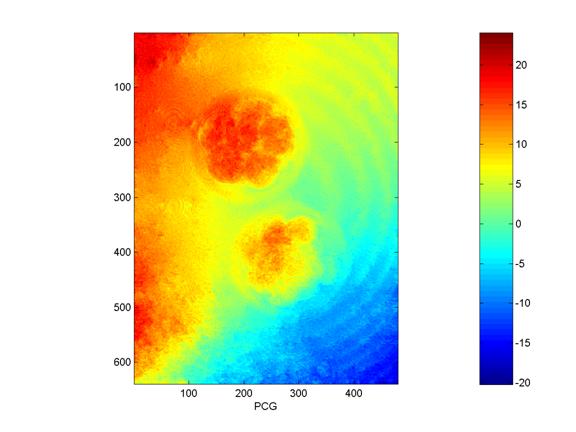
Figure 6: Preconditioned Conjugate Gradient (PCG) algorithm

The PCG method produces a reasonably good unwrapping except for the tendency to accumulate the phase from one corner of the image to another. In Figure 6 it can be seen that at (0, 0) the phase is near maximum while at (480,640) the phase value is at a minimum. The embryos are clearly visible although individual cell boundaries and the membrane of the zona pellucida are vague. This method takes on the order of seconds to execute.

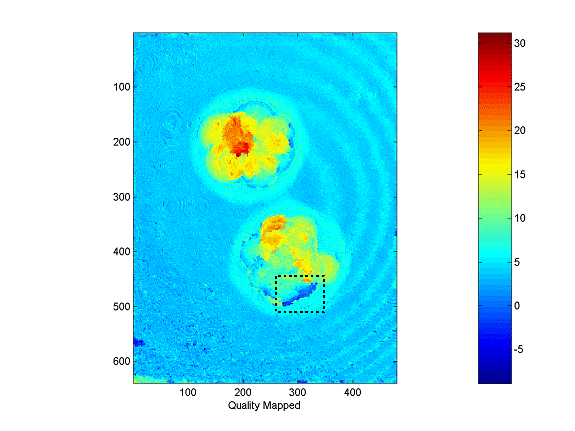
3.6 Quality Mapped

Figure 7: Quality Mapped unwrap

The quality mapped solution shown above has regions where the unwrap fails. For example, within the dotted box the cell boundaries show up as a decrease in phase rather than an increase. This method takes a few seconds to execute.

3.7 Flynn’s Algorithm

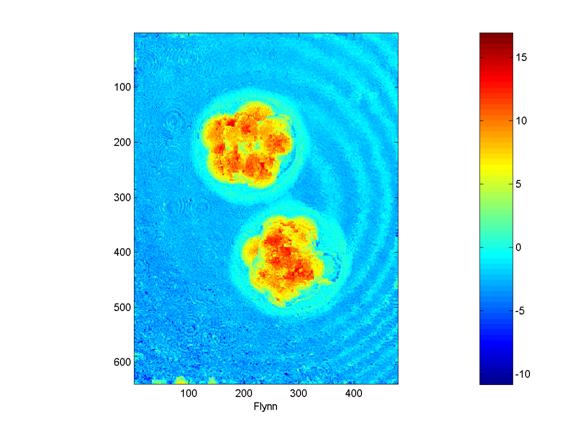
Figure 8: Flynn’s minimum discontinuity algorithm

Flynn’s algorithm produces a significantly better result than the quality mapped algorithm. However, the solution can still be seen as incorrect given that the thickness of the sample should be increasing as the sample is traversed from the edge of the zona to the center of the embryo. The actual solution varies back and forth between 0 and 15 however once the first cell wall is reached, rather than changing in a non-decreasing fashion. Some cell boundaries also show up as phase decreases rather than increases. This algorithm takes less than a minute to run.

3.8 Minimum L^P-Norm

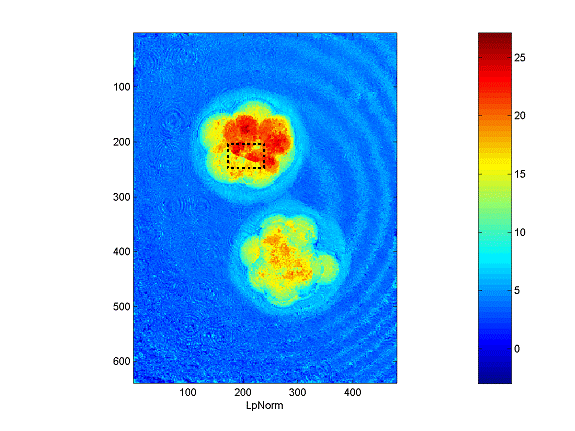
Figure 9: Minimum L^PNorm (p=0)

Visually, the minimum L^PNorm algorithm produces the best solution. There are still segments that are incorrect (such as that within the dotted box) but overall, this is the most discontinuity-free solution. Average background noise is also minimized in comparison to the other algorithms. However, this is the second slowest algorithm and usually takes a few minutes to execute (actual execution time is dependent on the speed of convergence and can vary greatly)

4.0 Conclusions

The two criteria upon which the different algorithms can be judged are:

1) Quality: This ensures that the unwrapping is as close to correct as possible. It is therefore the most important criteria.

2) Performance: This is a measure of the speed with which the various unwrapped images are produced. This is the aspect to be optimized via a hardware implementation. It is important since a sufficiently fast software implementation would not require hardware.

Space was not considered since current workstations have sufficient amounts of RAM to hold all image arrays in memory simultaneously.

The unwrapping algorithms that produce the best quality results are Flynn’s and the minimum L^P Norm. Flynn’s algorithm takes less than one minute while L^PNorm takes several minutes. Neither one is fast enough for a purely software implementation. The L^PNorm algorithm was finally chosen since it consistently produces a slightly better unwrap than Flynn’s algorithm although it takes several times as long.

REFERENCES

[1] Warger, W. C., Newmark, J., Zhao, B., Warner, C., DiMarzio, C. A. Accurate cell counts in live mouse embryos using optical quadrature and differential interference contrast microscopy, SPIE, February 2006.

[2] D. C. Ghiglia and M. D. Pritt, Two-Dimensional Phase Unwrapping: Theory, Algorithms and Software, John Wiley & Sons, 1998.

[3] Smith, C. An investigation of two-dimensional phase-unwrapping algorithms, Master’s Project, Northeastern University, 2003.

Further unwrapped images taken with the Keck microscope and with the separate OQM setup are available at http://www.coe.neu.edu/~sbraganz/images