GPU Acceleration in a Modern Problem Solving Environment: SCIRun's Linear System Solvers

Devon Yablonski, Miriam Leeser

Abstract

   This research demonstrates the incorporation of GPU’s parallel processing architecture into the SCIRun biomedical problem solving environment with minimal changes to the environment or user experience. SCIRun, developed at the University of Utah, allows scientists to interactively construct many different types of biomedical simulations. We use this environment to demonstrate the effectiveness of the GPU by accelerating time consuming algorithms present in these simulations. Specifically, we target the linear solver module, which contains multiple solvers that benefit from GPU hardware. We have created a class to accelerate the conjugate gradient, Jacobi and minimal residual linear solvers; the results demonstrate that the GPU can provide acceleration in this environment. A principal focus was to remain transparent by retaining the user friendly experience to the scientist using SCIRun’s graphical user interface. NVIDIA’s CUDA C language is used to enable performance on NVIDIA GPUs. Challenges include manipulating the sparse data processed by these algorithms and communicating with the SCIRun interface. Our solution makes it possible to implement GPU versions of the existing SCIRun algorithms easily and can be applied to other parallel algorithms quickly. The GPU executes the matrix and vector arithmetic to achieve acceleration performance of up to 16x on the algorithms in comparison to SCIRun’s existing multithreaded CPU implementation. The source code will be incorporated and publicly available in future versions of SCIRun.

Overview

    SCIRun is a biomedical problem solving environment that gives the user a graphical interface in which they may create simulations and computations in an intuitive way. Developed by the SCI group at the University of Utah, SCIRun is available to download as open source software at SCIRun website. "Modules" are selected and placed on the work space as desired, and their inputs and outputs are routed as desired.

    An example use of SCIRun is the Heart Ischemia model. This model is a simulation based on real imaging data of a dog heart that has damaged tissue. Performing an algorithm on the data can create a 3D image of the electrocardiac potentials in the tissue, allowing medical personnel to analyze and further diagnose the damage. Figures 1 and 2 shows the SCIRun network for this model and the output.

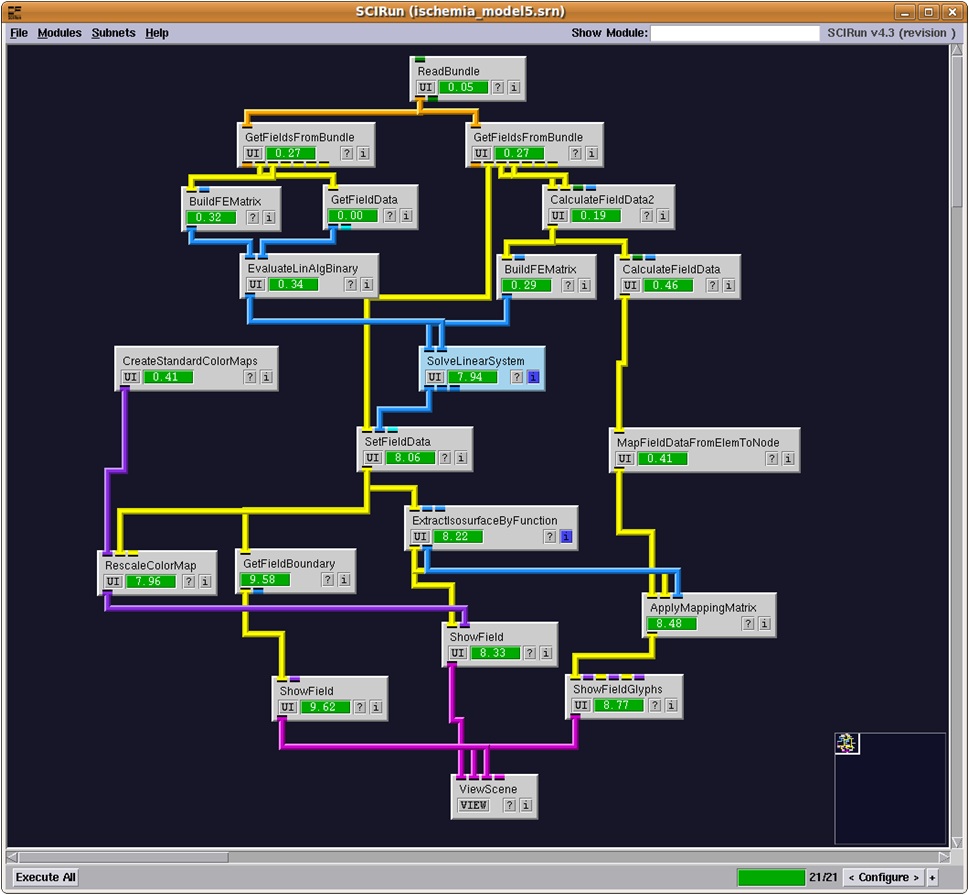
Figure 1: SCIRun interface and Heart Ischemia network

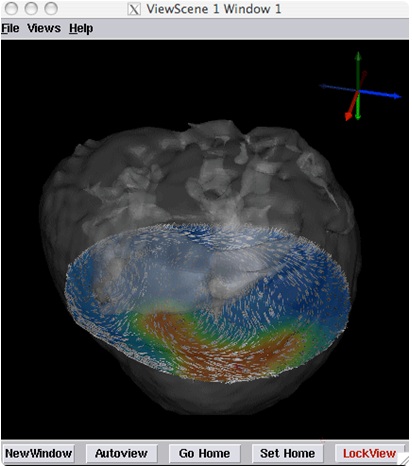
Figure 2: 3D heart image generated by the model

    The data contained in this model is a large sparse matrix (107K x 107K square matrix) with over 1 million double precision nonzero values. Many of the algorithms to be performed on this data will be time consuming due to the raw size of the data and contain ample parallelism to allow acceleration on modern parallel architectures. The scientist using SCIRun would benefit from an acceleration of these algorithms through greater productivity potentially leading to an earlier diagnosis or saving a life. This was the motivation of our work - accelerating algorithms in SCIRun with GPGPUs while remaining transparent to the scientist.

    In order to design a modular GPU solution within the SCIRun environment, an example algorithm already existing in the program was chosen - the linear solver in the "SolveLinearSystem" module. This module exists in the center of the heart ischemia model (Figure 1). Figure 3 shows the user interface of the module.

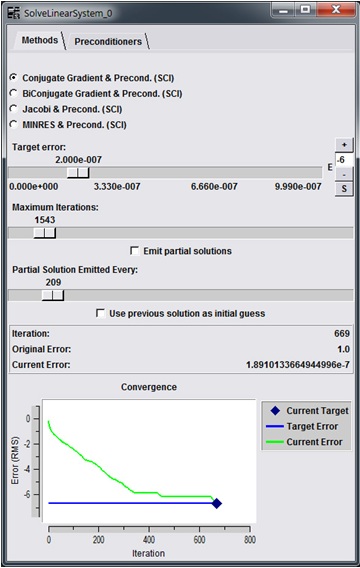
Figure 3: SolveLinearSystem module user interface

    The interface features several paremeters of the algorithm that the user can modify. Towards the bottom of the interface is a graphical output of the convergence of the algorithm that is updated in real time during computation. This presents one of the challenges of implementing GPGPU in problem solving environments. It is required to off-load data to the GPU during computation and any communications with the host software involves transferring the desired data back, which results in a drop in performance. Our goal is to demonstrate that the GPU can be used effectively for acceleration even while incurring such penalties.

GPU

    Over the last several years, graphics processors have been an attractive accelerator due to its many-core hardware both in academia and industry. The reason for this trend is due to the work done to make the hardware accessible to programmers for computation other than graphics through programming language extensions such as CUDA C and OpenCL. GPUs have many homogeneous cores that operate single instructions across parallel data (SIMD). The NVIDIA CUDA (the architecture used in this project) GPU memory layout and core configuration is shown in Figure 4.

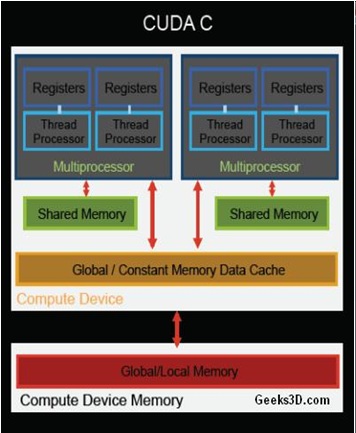
Figure 4: NVIDIA Architecture

NVIDIA GTX 280 GPU Characteristics

• SIMD → Single Instruction performed across Multiple Data
• 240 Cores → 32 multiprocessors (MP) delegate instructions to 8 cores each
• Multi-tiered memory layout → 1GB global, 16kB shared, 16384 registers per MP
• Multi-threading → 32 threads in a "warp" are delegated to each core
• Ease of programming → Programmable using NVIDIA CUDA C or OpenCL

Design

    The linear solving module in SCIRun contains multiple common linear solving algorithms, such as the conjugate gradient, minimal residual and Jacobi methods. Our implementation is intended to be accessible to all of these algorithms and also to other algorithms throughout SCIRun. The GPU was implemented in a library style that performs small vector and matrix (linear algebra) mathematics and will be accessible throughout SCIRun. We trade-off the possible increased performance possible in computing the entire algorithm in a single GPU program for the lower granularity approach that allows us to communicate data back to the host during computation. This allows us to provide data to the host to update visual updates in the environment - the GPU implementation is transparent in SCIRun while performing the algorithm faster.

    As an example of the parallelism available, the conjugate gradient algorithm contains nearly all vector and matrix computations in each iteration. Figure 5 shows the vector operations accelerated in green rectangles and SPMV computations in blue ovals.

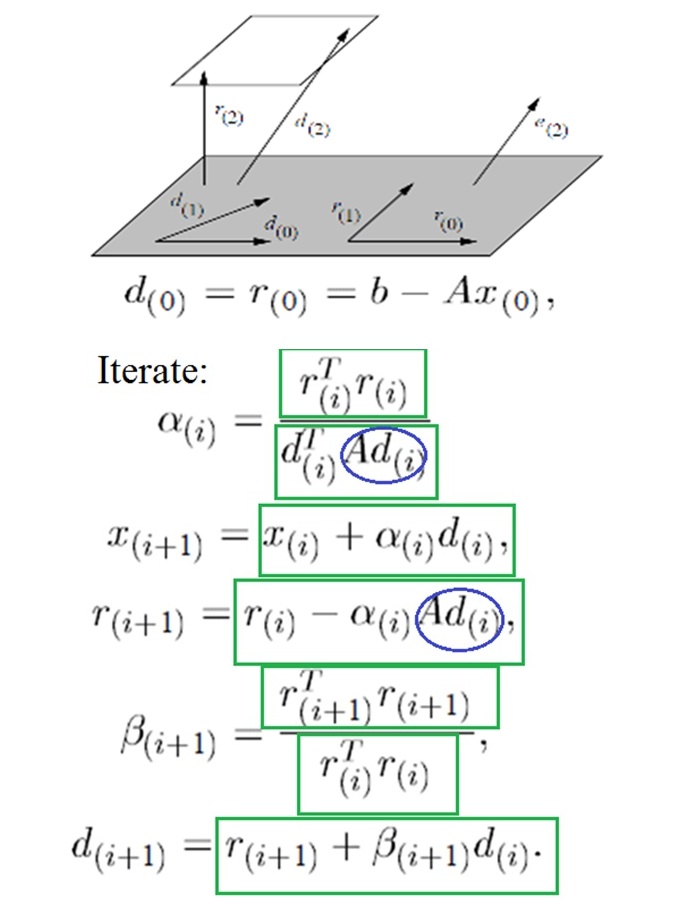
Figure 5: Conjugate Gradient Parallelism

    SCIRun is an open souce software that encourages the user to add any desired algorithms or modules for personal use and for distribution to other users and future releases of the software. To facilitate this, they designed the software in an abstract hierarchy that allows a scientist with only limited programming experience design their algorithm. For instance, the SolveLinearSystem module has the algorithm written at a high level (on the order of simply declaring a multiply between a vector and a matrix) and the low level actual data manipulation happens in a separate file, reused for other algorithms. Our GPULinearAlgebra class mimics the CPU linear algebra functions allowing the scientist to program for the GPU with no understanding of the underlying hardware. Figure 6 shows the layout of our design and Figure 7 shows the ease of which algorithms can be converted or written for the GPU.

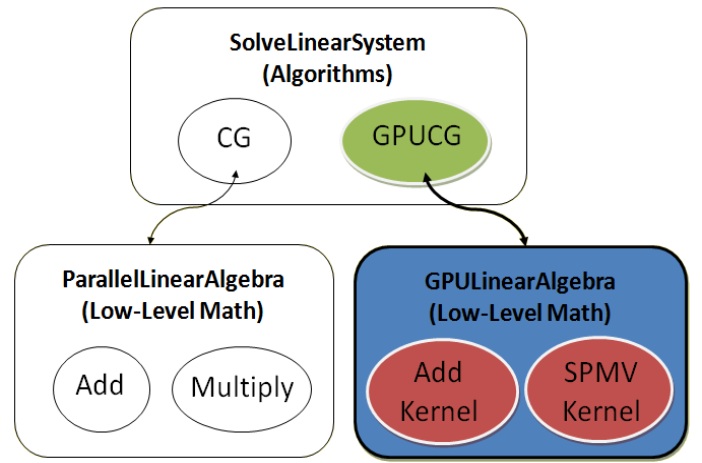
Figure 6: GPULinearAlgebra

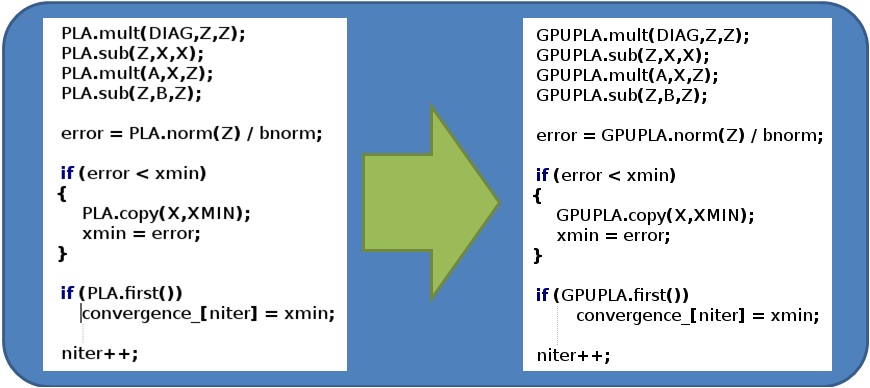
Figure 7: Programmming paradigm demonstrated in Jacobi Method

Results

    We tested the heart ischemia model and also a collection of sparse matrices provided by the University of Florida's Sparse Matrix collection using our GPU implementation. The sizes of the data range from 6.3K to 3.5 million rows and have up to 14.8 million nonzero values. We achieved up to 16x speedup of the conjugate gradient algorithm on the largest examples in comparison to the CPU execution time while providing the same user experience (Figure 6). Our results are comparable to other double precision sparse linear solvers available while retaining communication with the graphical interface throughout the computation.

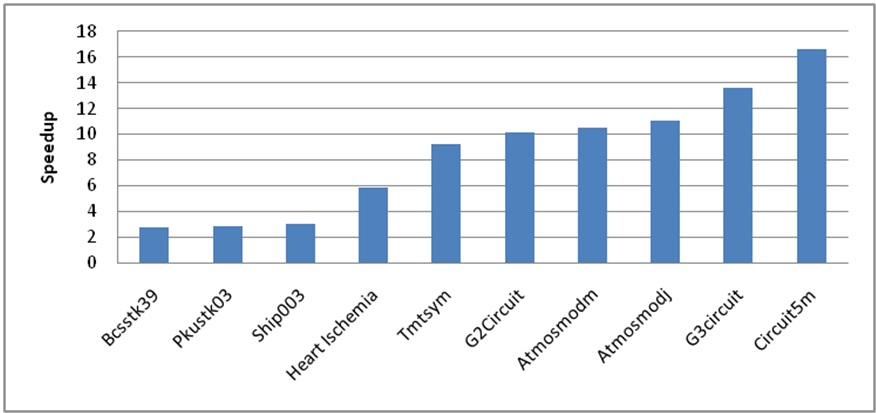
Figure 8: Conjugate gradient speedup results

    We also have implemented and tested the Minimal Residual and Jacobi methods as well. Our speedup is demonstrated on the heart ischemia model in Figure 9.

Figure 9: Speedup of Minimal Residual and Jacobi Methods

    Finally, there are a few additions to the SolveLinearSystem module that allow the GPU version to be used (Figure 10). These additions are:

• a.) Use GPU check box that allows user selectable GPU acceleration
• b.) A slider bar allowing to change how often the visual graph is updated. This improves the performance for both the CPU and GPU versions.
• c.) An output of the previous run execution time for comparing GPU and CPU performance

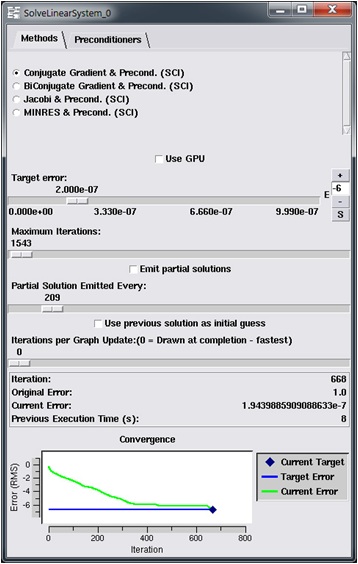
Figure 10: Updated SolveLinearSystem module

Devon Yablonski - 2010 - yablonski.d@husky.neu.edu